Bagi Anda yang gemar pelajaran matematika, tentu Anda sudah tidak asing lagi dengan aritmatika. Aritmatika adalah salah satu cabang matematika yang mempelajari sifat-sifat dan hubungan antar bilangan, terutama dalam operasi seperti penjumlahan, pengurangan, perkalian dan pembagian. Aritmatika juga biasanya dikenal dengan barisan dan deret. Barisan aritmatika adalah urutan bilangan di mana setiap suku diperoleh dengan menambahkan selisih tetap ke suku sebelumnya, sedangkan deret aritmatika adalah hasil penjumlahan suku-suku dari barisan aritmatika tersebut.

Jadi bisa juga disimpulkan bahwa perbedaan keduanya yaitu, barisan aritmatika berfokus pada urutan bilangan. Sedangkan deret aritmatika melibatkan penjumlahan bilangan dalam urutan tersebut. Untuk Anda yang ingin mempelajari lebih dalam mengenai aritmatika, berikut merupakan beberapa rumus, contoh soal beserta pembahasannya yang dapat Anda jadikan sebagai bahan latihan untuk mengerjakan ujian atau sebagainya.

Lihat Juga : Contoh Soal Sinonim dan Antonim

Rumus Barisan Aritmatika

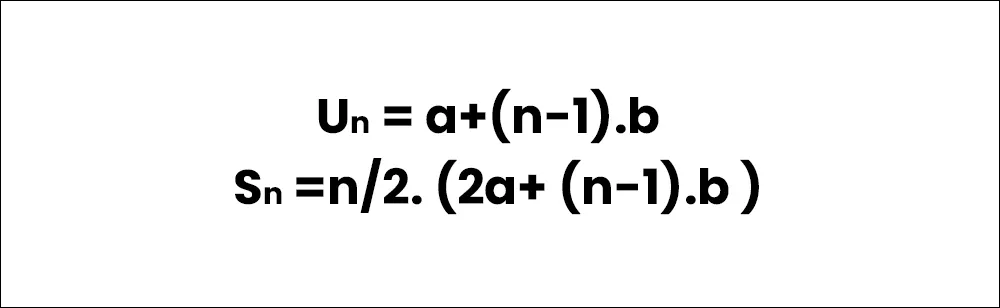
Beberapa dari Anda mungkin masih belum tahu bagaimana cara mengerjakan soal aritmatika dan apa saja rumus yang digunakan untuk mengerjakannya. Berikut merupakan beberapa rumus yang biasanya digunakan untuk menghitung aritmatika.

Rumus umum untuk suku ke-n dalam sebuah barisan aritmetika adalah?

U_n = a+(n-1).b

Di mana :

• U_n adalah suku ke-n
• a₁ adalah suku pertama
• n adalah urutan suku yang dicari, dan
• b adalah selisih antar suku (beda)

Selain itu, rumus untuk menghitung jumlah Sn dari n suku pertama dalam barisan aritmetika adalah:

Sn =n/2. (2a+ (n-1).b )

Semua nilai di atas harus diisi dengan nilai yang sesuai untuk mendapatkan hasil yang sesuai.

Lihat Juga : Contoh soal Psikotes Deret Angka

Contoh Soal Barisan Aritmatika Beserta Jawaban dan Pembahasannya

Untuk lebih jelasnya sebaiknya Anda berlatih beberapa soal agar lebih mudah memahami bagaimana mengerjakan soal barisan aritmatika. Adapun beberapa contoh soal yang dapat Anda simak yaitu sebagai berikut.

Contoh Soal Pilihan Ganda Barisan Aritmatika

1. Diketahui barisan aritmatika: 2, 6, 10, … Tentukan suku ke-14 !

A. 52
B. 54
C. 56
D. 58

Jawaban: B

2. Suku ke-25 dari barisan 1, 3, 5, 7, … adalah ?

A. 37
B. 39
C. 47
D. 49

Jawaban: D

3. Suku ke-55 dari barisan bilangan 7, 15, 23, 31, 39, … adalah ?

A. 496
B. 488
C. 447
D. 439

Jawaban: D

4. Suku ke-n dari barisan 2, 6, 12, 20, 30, … adalah ?

A. n2 + 1
B. 4n – 2
C. n(n + 1) 
D. 3n – 1

Jawaban: C

5. Empat suku berikutnya dari barisan 1, 3, 6, 10 … adalah ?

A. 16, 23, 31, 40
B. 16, 34, 44, 56
C. 15, 20, 26, 33
D. 15, 21, 28, 36

Jawaban: D

6. Pada susunan bilangan-bilangan segitiga pascal, jumlah bilangan yang terdapat pada baris ke-10 adalah…

A. 128
B. 256
C. 512
D. 1.024

Jawaban: C.

7. Diketahui suku ke-11 suatu barisan aritmatika adalah -16 dan suku ke-20 adalah -34. Suku kelima belasnya adalah…

A. -28
B. -24
C. 24
D. 30

Jawaban: B

8. Suatu barisan aritmatika diketahui mempunyai a = 6 dan U10 = 20. Jumlah suku-sukunya adalah…

A. 130
B. 120
C. 20
D. 30

Jawaban: A 

9. Pada suatu barisan siswa SMP Bakti, barisan paling depan diisi oleh 5 orang siswa, barisan belakangnya 8 orang siswa, barisan berikutnya 11 orang siswa dan seterusnya. Berapakah jumlah siswa pada barisan ke-10?

A. 27
B. 32
C. 35
D. 47

Jawaban: B

10. Pada suatu ruangan rapat, disusun kursi dengan baris depan 12 kursi, baris kedua 14 kursi, baris ketiga 16 kursi. Maka banyaknya kursi di baris ke 5 adalah …

A. 18
B. 20
C. 22
D. 24

Jawaban: B

11. Sisi-sisi segitiga siku-siku membentuk barisan aritmatika. Jika sisi terpendek 24 cm, panjang sisi siku-siku yang lain adalah…

A. 36 cm
B. 34 cm
C. 32 cm
D. 28 cm

Jawaban: C

12. Rumus suku ke-n dari barisan 3, –2, –7, –12, … adalah …

A. 4an + 1
B. 5an – 8
C. -5an +8
D. -2an² -1

Jawaban: C

13. Pada barisan aritmatika 7, 5, 3, 1, suku ke 20-nya adalah …

A. -31
B. 31
C. 38
D. 45

Jawaban: A

14. Contoh soal barisan aritmatika SMA beserta pembahasannya, pada suatu barisan aritmatika 10, 6, 2, -2, -6, -10. Berapakah beda barisan tersebut?

A. – 4
B. 4
C. -6
D. 6

Jawaban: A

15. Suku keempat dan kesepuluh dari suatu barisan aritmatika berturut-turut adalah 21 dan 51. Rumus suku ke-n barisan aritmatika yaitu:

A. 1 + 5n
B. 6 + 5n
C. 6 + 5n – 5
D. 5n + 1

Jawaban: D

16. Hitunglah beda dari barisan berikut: 3, 6, 9.

A. 5
B. 6
C. 2
D. 3

Jawaban: D

17. Hitunglah besarnya U32 dari barisan 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, … !

A. 54
B. 69
C. 29
D. 36

 Jawaban: B

18. Tentukan suku tengah dari barisan 9, 11, 13, 15, 17,…69.

A. 24
B. 38
C. 29
D. 39

Jawaban: D

19. Diketahui suatu barisan aritmetika dengan suku pertamanya –15 dan suku kelimanya 1. Tentukan beda barisan aritmetika tersebut, tentukan suku kesepuluh barisan aritmetika tersebut, dan tuliskan 10 suku pertama barisan aritmetika tersebut adalah?

A. 24
B. 21
C. 23
D. 31

Jawaban: B

20. Diketahui barisan Aritmatika : 2, 6, 10,… Tentukanlah suku ke-14

A. 54
B. 52
C. 53
D. 51

Jawaban: A

21. Rumus umum suku ke-n dari barisan bilangan 2, 4, 8, 16, 32, .. adalah?

A. 2ⁿ
B. 2n + 2
C. 2n²
D. 2n -2

Jawaban: A

22. Diketahui sebuah barisan bilangan 5,9, 13, 17, …. rumus suku ke-n dari barisan bilangan tersebut adalah?

A. Un = 4 + n
B. Un = 3 + 2n
C. Un = 2 + 3n
D. Un = 1 + 4n

Jawaban: D

23. Suku ke-5 dan suku ke-8 suatu barisan aritmetika berturut – turut yaitu 22 dan 34. Jumlah n suku pertama barisan tersebut adalah?

A. 4n + 2
B. 4n – 2
C. 4n + 10
D. 2n² + 4n

Jawaban: D

24. Jumlah 6 suku pertama dari deret ½ + ¼ = 1/8 + …. adalah?

A. 63/64
B. 64/3
C. 64/3
D. -64/63

Jawaban: A

25. Suku ke-3 dan ke-8 sebuah barisan aritmatika diketahui barisan aritmetika diketahui berturut – turut 20 dan 40. Suku pertama dan beda barisan aritmatika tersebut berturut – turut adalah

A. 4 dan 12
B. 12 dan 4
C. -12 dan 4
D. 3 dan 9

Jawaban: B

26. Lima suku pertama dari barisan aritmatika yang diketahui rumus umum suku ke-n Noya Un = 3n + 3 adalah?

A. 3, 6, 9, 12, 15
B. 4, 7, 11, 15, 18
C. 6, 9, 12, 15, 18
D. 0, 3, 6, 9, 12

Jawaban: C

27. Rumus yang benar untuk suku ke-n dari barisan aritmatika 4, 10, 16, …. adalah ?

A. 4 + 6n
B. 4 + 3n
C. 4 + 2n
D. 6n – 2

Jawaban: D

28. Suku ke-40 dari barisan 7, 5, 3, 1 adalah?

A. 71
B. 54
C. -71
D. 39

Jawaban: C

29. Suku ke-24 dari barisan aritmetika 6, 9, 12, 15 adalah?

A. 65
B. 75
C. 85
D. 95

Jawaban: B

30. Suatu barisan aritmatika adalah 2, 6, 10, ….. maka suku ke-14 adalah?

A. 52
B. 54
C. 56
D. 58

Jawaban: B

Lihat Juga : Contoh Soal TKD dan Value Core BUMN

Contoh Soal Essay Barisan Aritmatika

Selain berupa soal pilihan ganda, Anda juga bisa berlatih untuk mengerjakan soal essay. Beberapa soal essay di bawah ini juga sudah lengkap dengan pembahasan atau cara mengerjakannya sehingga lebih memudahkan Anda untuk mengetahui bagaimana cara menyelesaikannya. Contoh soalnya yaitu antara lain sebagai berikut:

1. Suatu barisan aritmatika memiliki 8 suku. Apabila suku ke 3 adalah 50, dan suku ke 6 adalah 95, maka berapa beda barisan tersebut?

Jawaban: 15

Pembahasan:

Diketahui:

a3 = 50
a6 = 95

Rumus:

an = a + (n – 1).b

Pertama, Anda susun terlebih dahulu persamaan untuk suku yang diketahui:

a3 = a + (3 – 1).b
50 = a + 2b 
50 – 2b = a ->

a = 50 – 2b (persamaan 1)

Selanjutnya, susun persamaan untuk suku ke 6:

a6 = a + (6 – 1).b
95 = a + 5b ->

a + 5b = 95 (persamaan 2)

Setelah itu substitusikan persamaan 1 ke persamaan 2:

a + 5b = 95
(50 – 2b) + 5b = 95
– 2b + 5b = 95 –50
3b = 45
b = 15

Maka beda barisan tersebut adalah 15.

2. Pada suatu barisan Aritmetika diketahui U8 = 24 dan U10 = 30.

Tentukan:

a. Beda dan suku pertamanya
b. Suku ke-12
c. 6 suku yang pertama

Jawaban: a. Beda = 3, b Suku ke 12 = 36, c. 6 suku yang pertama adalah 3, 6, 9, 12, 15, 18

Pembahasan:

Diketahui:

U10 = a + 9b = 30
U8 = a + 7b = 24

Penyelesaian:

(eliminasi U10 dengan U8)

2b = 6
b = 3

U8 = a + 7b = 24
a + 7(3) = 24
a + 21 = 24
a = 3

– Jadi didapat beda = 3 dan suku pertama = 3

Un = a + (n – 1)b
U12 = 3 + (12 – 1)3
U12 = 3 + 11 . 3
U12 = 36

Jadi enam suku yang pertama adalah 3, 6, 9, 12, 15, 18

3. Apabila suku pertama pada suatu barisan adalah 1, dan suku kedua 3, maka suku ke-10 ialah: 

Jawaban: 19

Pembahasan:

Diketahui:

a1 = 1
a2 = 3
b = a2 – a1
b = 3 – 1
b = 2

Rumus:

an = a + (n-1).b
a10 = 1 + (10 – 1).2
a10 = 1 + (9) 2 
a10 = 1 + 18 
a10 = 19

Jawaban: Jadi suku ke-10 pada barisan aritmatika di atas yaitu 19

4. Suatu barisan memiliki suku 5, 8, 11, … . Tentukan nilai dari suku ke-15!

Jawaban: 47

Pembahasan:

Diketahui:

a1 = 5
a2 = 8
b = a2 – a1
b = 8 – 5
b = 3

Rumus:

an = a + (n-1).b
a15 = 5 + (15-1).3
a15 = 5 + 14.3
a15 = 5 + 42
a15 = 47

Oleh karena itu, nilai dari suku ke-15 adalah 47.

5. Apabila suatu barisan aritmatika memiliki suku pertama 4, dan suku ke 20 adalah 61, maka berapa nilai perbedaan barisan tersebut?

Jawaban: 3

Pembahasan:

Diketahui:

a = 4
a20 = 61

Rumus:

an = a + (n-1).b
a20 = 4 + (20-1).b
a20 = 61 19 b
a20 = 61 – 4
a20 = 57 b 
a20 = 57/19
b = 3

Nilai perbedaan antar suku pada barisan tersebut adalah 3.

6. Beberapa suku yang diketahui pada suatu barisan aritmatika yaitu: 2, 6, 10, … . Maka suku ke-14nya adalah:

Jawaban: 54

Pembahasan:

Diketahui:

a = 2
b = a2 – a1
b = 6 – 2
b = 4
n = 14

Rumus:

an = a + (n – 1).b
a14 = 2 + (14 – 1).4
a14 = 2 + 13 . 4
a14 = 2 + 52 
a14 = 54

Jadi jawaban dari  barisan aritmatika tersebut yaitu 54.

7. Pada tahun pertama sebuah butik memproduksi 400 stel jas Setiap tahun rata-rata produksinya bertambah 25 stel jas Berapakah banyaknya stel jas yang diproduksi pada tahun ke-5 ?

Jawaban: 500 setel jas

Pembahasan:

Diketahui:

Banyaknya produksi tahun I, II, III, dan seterusnya membentuk barisan aritmetika yaitu 400, 425, 450, ….

a = 400 dan b = 25

Ditanyakan: U5=?

Penyelesaian:

U5 = a + (5 – 1)b
= 400 + 4 . 25
= 400 + 100
= 500

Jadi banyaknya produksi pada tahun ke-5 adalah 500 stel jas

8. Diketahui barisan Aritmetika : 2, 6, 10, …. Tentukan suku ke-14

Jawaban: 54

Pembahasan:

Diketahui:

a = 2
b = 6 – 2 = 4

Ditanyakan:

U14=?

Penyelesaian:

Un = a + (n – 1)b
U14 = 2 + (14 – 1).4
= 2 + 13 . 4
= 2 + 52
= 54

9. Suku ketiga suatu barisan aritmatika adalah 10. Jika jumlah suku kelima dan suku ketujuh barisan aritmatika tersebut adalah 38, suku kedua adalah ….?

Jawaban: 7

Pembahasan:

U3 -> a + 2b = 10…(1)
U5 + U7 -> (a + 4b) + (a + 6b) = 38
U5 + U7 -> 2 a + 10b = 38
=> a + 5b = 19…(2)

Dari (1) dan (2):

a + 2b = 10
a + 5b = 19 (-)
-3b = -9
b = 3

a + 2b = 10
a + 2(3) = 10
a = 4

U2 = a + b
U2 = 4 + 3
U2 = 7

10. Diketahui satu barisan aritmatika dengan U2 + U3 + U4 = 24. Jika banyak suku barisan adalah 21 dan suku tengahnya adalah 24, suku ke-21 = ….

Jawaban: 44

Pembahasan:

U2 + U3 + U4 = 24
(a + b) + (a + 2b) + (a + 3b) = 24
3a + 6b = 24
a + 2b = 8… (1)

n = 21 -> suku tenah Ut adalah
suku ke- (21 + 1)/2 = U11
U11 = a + 10b =24… (2)

Dari (1) dan (2):

a + 2b = 8
a + 10b = 24 (-)
-8b = -16
b = 2

a + 2b = 8
a + 2(2) = 8
a = 4

U21 = a + 20b
U2 = 4 + 40
U2 = 44

Lihat Juga : Contoh Soal Eksponen

Penutup

Tujuan belajar aritmatika melibatkan pengembangan kemampuan dasar dalam berbagai aspek matematika. Hal ini termasuk pemahaman konsep angka, operasi dasar, keterampilan berhitung, dan kemampuan memecahkan masalah matematika sederhana. Aritmatika membentuk dasar yang penting untuk pemahaman matematika yang lebih kompleks di tingkat selanjutnya.

Selain itu, jika Anda terus-menerus berlatih mengerjakan soal aritmatika dan mampu menguasainya, maka Anda tidak hanya mampu mengerjakan soal ujian dengan mudah. Namun aritmatika juga akan membantu Anda dalam kehidupan sehari-hari, seperti berbelanja, mengelola keuangan, dan membuat keputusan praktis lainnya.

---

Penulis : Adella Eka Ridwanti | Editor : Rudi Dian Arifin, Wahyu Setia Bintara